

어떤 컴퓨터 관련 수업이든 처음은 bit의 이해부터 시작한다. bit(binary digit)는 컴퓨터 안에서 정보를 나타내기 위한 최소 구성 단위로, 0과 1로 이루어져 있다. 여기까지만 들었을 때 '0, 1로 이루어진 숫자구나'라고 생각하기 쉽지만 사실 전류가 끊겼다 이어졌다 하는 전기적인 신호를 우리가 알아보기 쉽게 0과 1로 나타낸 것 뿐이다. 그래서 bit를 0, 1로 나타낸 것과 마찬가지로 False, True로 나타낼 수도 있다.
아무튼 컴퓨터는 비트의 패턴(Patterns of bits)들을 이용해서 정보를 표현한다. 이 비트의 패턴, 즉 정보는 알파벳과 같은 문자를 나타낼 수도 있고 이미지나 소리를 나타낼 수도 있다.
01. 부울 연산(Boolean Operations)
논리(logic)라는 수학 분야를 개척한 부울(George Boole, 1815-1864)을 기념하기 위해 참/거짓을 다루는 연산을 부울 연산이라고 부른다.
세 가지 기본 부울 연산은 AND, OR, XOR(eXclusive OR, 배타적 논리합)이다. 두 값을 연산해 제3의 결과를 만들어낸다는 점에서 덧셈, 곱셈 등과 비슷하다.

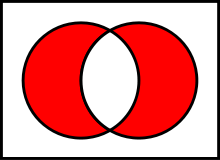
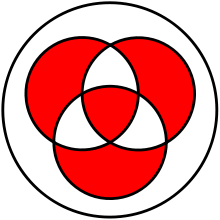
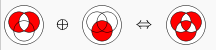
여기서 AND, OR은 비교적 흔하게 접했겠지만 XOR은 조금 생소할 수 있다. XOR은 주어진 2개의 명제 가운데 1개만 참일 경우를 판단하는 논리 연산으로 AND나 OR과는 조금 다르다. 아래 벤 다이어그램을 확인하면 더 이해하기 쉽다.
02. 게이트와 플립플롭(Gates and Flip-Flops)
이제 0, 1을 이용해 제3의 값을 얻는 부울 연산이라는 이론적인 부분을 확인했으니 실제 세상에서 우리가 사용하는 방식을 알아보자.
부울 연산의 입력 값들이 주어질 때 연산 결과를 출력하는 장치를 게이트(Gate) 혹은 논리 게이트(Logic Gate)라고 부른다.
게이트는 오른쪽으로 돌면 1, 왼쪽으로 돌면 0을 의미할 수 있는 톱니바퀴부터 낮은 전력의 계전기에 사용되는 릴레이(relay), 파동의 간섭에 의해 보강되거나 소멸되는 빛을 이용한 광학 장치(optical gate) 등을 이용해 만들 수 있다. 기술이 발전해서 오늘날의 컴퓨터에서 사용되는 게이트는 전압 차이로 0, 1을 구분 지을 수 있는 트랜지스터(Transistor)를 주로 사용한다. 참고로 양자 컴퓨터 같은 경우는 트랜지스터 대신 0, 1, 중첩 상태를 표현할 수 있는 양자를 사용한다.

위에 보이는 것처럼 트랜지스터의 다리는 최소 3개 이상으로 구성되어 있으며 왼쪽부터 emitter, base, collector라고 한다. 각설하고 이 트랜지스터를 한개 혹은 여러 개를 다양한 방식으로 연결하고 각 base에 전압을 걸어주거나(1) 걸어주지 않(0)으면 그에 따른 결과로 전류가 흐르거나(1) 흐르지 않(0)는다. 이 연결하는 방식에 따라 AND, OR, XOR, NOT 등의 다양한 부울 연산을 할 수 있다.

위의 그림처럼 A, B에 전압을 통해 각각 0 혹은 1의 신호를 주면 Q에서 결과값이 나온다. 전기 신호이기 때문에 입력값이 사라지면 출력값이 유지되지 않는다. 즉, AND게이트의 A, B에 각각 1의 신호를 걸어 Q에 1이라는 결과값을 얻었다 하더라도 입력값이 사라지면 그 이후에는 Q에 1이 들어왔었는지 0이 들어왔었는지 알 수 없다는 것이다.
하지만 이와 같은 게이트들을 또 다시 여러개를 연결하면 입력값을 한번 주고 끊어도 그 결과값이 유지될 수 있다. 이 게이트들의 조합을 플립플롭(Flip-Flop)이라고 하며 컴퓨터 메모리의 기본 단위가 된다. 플립플롭은 0 혹은 1을 출력 값으로 가지며, 다른 회로로부터 출력 값을 변경하라는 펄스 신호가 올 때까지 기존의 출력 값을 일정하게 유지하는 회로다.

🎃참고
위의 그림은 아주 간단한 플립플롭 회로를 나타낸다. 위의 Input을 A라고 하고 아래를 B라고 하자. 초기에는 A, B에 둘다 어떠한 신호도 주고 있지 않다. 즉 A, B는 둘 다 0이다. 이 상태에서 A에 1을 걸면 A 앞에 있는 OR게이트의 출력값은 1이 된다. 따라서 Output이 1이 된다. 그 다음으로 아래에 있는 AND 게이트를 보자. 아까 OR게이트의 출력값이 다시 AND게이트의 입력값으로 오는데 그 값은 1이었다. 한편 B에서는 0이란 값을 유지하고 있었는데 B 앞의 NOT게이트를 통과하면 출력값이 1이 되고, 결국 AND 게이트의 출력값은 1이 된다. 따라서 OR게이트에서 두번째로 출력하는 값도 1이 된다. 이 상황에서 A의 입력값이 0으로 돌아간다하더라도 아래 AND 게이트에서 계속해서 출력값이 1이므로 Output은 1을 유지하게 된다.
결론적으로 플립플롭은 컴퓨터 안에서 하나의 비트를 저장하는 수단이다. 하지만 현대 컴퓨터의 메모리는 트랜지스터로 이루어져 있지는 않고, 실리콘 웨이퍼(wafer) 한 장 위에 수백만 개의 전기 회로들을 구성할 수 있는 VLSI(Very Large-Scale Integration, 초고밀도 집적회로)를 이용한 수백만 개의 플립플롭과 제어회로를 포함하는 소형 장치들로 이루어져 있다.
03. 16진법(Hexadecimal Notation)
컴퓨터는 0, 1로 이루어진 아주 긴 비트 패턴을 다룬다. 아주 긴 비트 패턴을 스트림(stream)이라고 부르는데, 컴퓨터에게 명령을 내리기 위해서 사람이 0100101101101010101110000010101...처럼 긴 스트림을 다뤄야 할까?
우리는 아주 긴 스트림의 표현을 쉽게 하기 위해 16진법이라는 간이 표기법을 사용한다. 왜 굳이 16진법이냐하면 비트 패턴의 길이가 대개 4의 배수라는 사실을 이용한 것이다. 4비트의 패턴을 표시할 때 16진법으로는 하나의 기호로 치환할 수 있다. 예를 들어 12비트의 패턴은 3개의 16진수 기호로 치환할 수 있는 것이다. 1101₍₂₎이라는 4비트 패턴은 10진법으로는 13₍₁₀₎이며, 이를 16진법으로는 D₍₁₆₎로 표시한다. 아래첨자를 지원하지 않는 텍스트 기반 언어로 프로그래밍하는 프로그래머들은 진법을 표시하기 위해 종종 접두사를 사용한다. 16진법의 표현을 명확히 하기 위해 "0x"라는 접두사를 사용할 수 있다.
비트 패턴이 길 경우 16진법의 위력을 좀 더 체험하기 쉬운데 10110110110101101010101011001010101001100101₍₂₎라는 비트 패턴은 16진법으로는 B6D6AACAA65₍₁₆₎로 표현된다.
'프로그래밍 > Computer Science' 카테고리의 다른 글
| [Overview] 01. Data Storage - (4) Data Compression (0) | 2023.07.14 |
|---|---|
| [Overview] 01. Data Storage - (3) The Binary System (0) | 2023.07.11 |
| [Overview] 01. Data Storage - (2) Main Memory (0) | 2023.07.11 |
| [알고리즘] 02. 에라토스테네스의 체 (4) | 2023.05.19 |
| [알고리즘] 01. 정렬 알고리즘(Sorting Algorithm) (2) | 2023.03.29 |
