

01. 2의 보수 ( Two's Complement )
02. 소수의 표현 ( Fractions in Binary )
0과 1로 표현되는 2진법 체계는 컴퓨터에서 보편적으로 사용된다. 2진법의 표기, 덧셈 같은 기초적인 내용은 건너 뛰도록 한다.
01. 2의 보수(Two's Complement)
2의 보수는 컴퓨터가 음수를 저장하기 위해 사용하는 정수 표현 체계 중에 하나이다.
4개의 bit로 구성된 머신이 있다고 하자. 이 머신은 2^4개의 경우의 수를 나타낼 수 있으므로 0 ~ 15 범위의 수를 저장할 수 있다. 하지만 음수를 표현해야 한다면 어떨까? 이를 위해서 범위의 절반을 음수에 할당한다. 그렇게 되면 4bit 머신의 경우 -8 ~ 7까지의 수를 저장할 수 있다. 또한 최상위 비트는 부호를 나타내는 부호 비트(sign bit)로 사용한다.
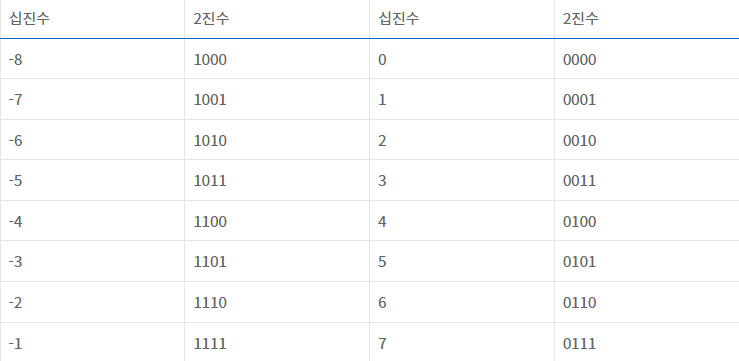
양의 값 7과 음의 값 -7 의 2진수 사이에는 한 관계가 있다. 모든 0을 1로 변경하고, 모든 1은 0으로 변경한 뒤 1을 더해주면 똑같다. 이를 다르게 표현하면 오른쪽 값에서부터 읽어나갈 때 첫번째 1을 만나기 전까지는 값을 그대로 유지하다가 1을 만난 후로 모든 값을 반대로 바꿔주는 것이다. 이런 변환 알고리즘을 사용하면 2진법에서 양수와 음수의 변환이 가능하다. 특히 이 방법을 사용하면 오른쪽에서 한번에 읽어나가면서 바꿔줄 수 있다.

2의 보수 표기법으로 표현된 두 수를 더하는 것은 기존 2진수의 덧셈과 동일하지만 마지막 올림수에 의해 결과의 왼쪽에 생기는 추가 비트는 절삭시키면 된다.
파이썬에서 2의 보수 체계를 테스트해봤다. 여기
오버플로(Overflow)
2진수의 덧셈의 결과가 할당된 비트 수로 표현할 수 있는 크기를 초과하는 경우 오버플로가 발생한다.
4bit 머신에서 2의 보수 체계로 나타낼 수 있는 최대값은 7이며, 최대 음수는 -8이다. 예를 들어 5 + 4를 연산할 경우 9라는 정확한 답을 얻을 수 없고 실제 결과는 -7을 나타낸다. 이처럼 계산결과가 표현될 수 있는 값의 범위를 벗어날 때 발생하는 문제를 오버플로라고 한다. 오늘날 2의 보수 표기법으로 값을 저장할 때 32비트를 사용하는 것이 일반적이며, 이 경우 2,147,483,647까지 오버플로 없이 결과를 나타낼 수 있다.
02. 소수의 표현(Fractions in Binary)
소수 즉, 정수를 넘어 실수를 2진법으로 표현할 때는 고정 소수점(Fixed Point)와 부동 소수점(Floating Point) 두 가지 방식이 있다.
실수는 정수와 달리 소수점을 기준으로 정수부와 소수부로 구분될 수 있다. 실수를 2진법으로 표현하는 방법은 정수에 비해 훨씬 복잡하다. 왜냐하면 컴퓨터는 0, 1만으로는 5.3, 0.1과 같은 실수를 정확히 표현할 수 없기 때문이다. 이를 최대한 정답에 가깝게 표현하기 위해 고정 소수점과 부동 소수점을 활용할 수 있다.
고정 소수점 (Fixed Point)
실수를 표현하는 가장 간단한 방식으로, 소수부의 자릿수를 정해놓고 고정된 자릿수에 소수를 표현하는 것이다.
실수를 32bit 머신에 고정 소수점 방식으로 표현하면 다음과 같다.
| sign bit(1bit) | 정수부(15bit) | 소수부(16bit) |
소수부에 할당된 bit가 16bit로 고정되어 있고 이 범위 안에서 값들을 표현할 수 있다. 소수부가 고정되어 있다는 것은 간단하다는 장점은 있지만 정밀한 숫자를 표현할 수 없다는 단점이 있다. 그렇다고 소수부의 bit를 늘리게 되면 정수부가 작아지므로 큰 숫자를 표현할 수 없게 되고, 정수부의 bit를 늘리게 되면 소수부에서 정밀한 숫자를 표현할 수 없어진다. 이러한 문제를 해결하기 위해 소수점을 고정하지 않고 소수를 표현하는 부동 소수점을 사용할 수 있다.
부동 소수점(Floating Point)
대부분의 시스템에서 사용하는 방식으로, 하나의 실수를 부호(sign), 가수(mantissa), 지수(exponent)로 나누어 표현한다.

고정 소수점 방식보다 더 넓은 범위의 수를 나타낼 수 있어 과학기술 계산 같은 정밀한 계산에 사용된다. 부동 소수점 방식의 경우에도 최상위 비트를 부호 비트로 정하고, 나머지를 지수 필드(exponent field)와 유효숫자 필드(mantissa field)로 나누어 사용한다.
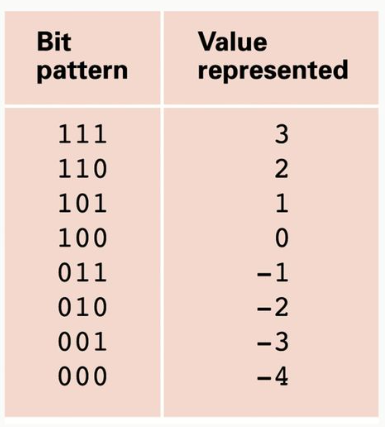
01101011₍₂₎이라는 1byte패턴으로 부동 소수점을 알아보자. 0은 부호 비트, 110은 지수, 1011은 유효숫자다. 우선 이 바이트를 해석할 때 1011₍₂₎이라는 유효숫자의 맨 왼쪽에 소수점을 붙여 .1011로 나타낸다. 그리고 나서 지수 부분인 110을 3비트 초과 표기법(excess notation)으로 해석한다. 초과 표기법에서는 최상위 비트가 1인 100₍₂₎을 0₍₁₀₎으로 기준 잡고 101₍₂₎은 1₍₁₀₎, 110₍₂₎은 2₍₁₀₎, 111₍₂₎은 3₍₁₀₎으로 나타낸다. 우리가 해석 중인 110₍₂₎은 2₍₁₀₎이므로 1byte패턴의 지수 부분은 2가 된다. 즉, 소수점의 위치를 오른쪽으로 2bit 옮기라는 뜻이다. 따라서 결과는 10.11이다.
이 결과를 십진수로 나타내면 2 + 3/4와 같으며 부호 비트는 양수인 0이므로 결론적으로 01101011 1byte패턴이 부동 소수점으로 해석한 2 + 3/4의 결과다.
반대로 부동소수점 표기법을 사용해 값을 저장하기 위해서는 위의 순서를 역으로 거슬러 간다. 예를 들어 1 + 5/8이라는 값을 인코딩하기 위해서는 먼저 정수와 소수를 각각 2진법으로 표현해 1.101을 얻는다. 그 다음 소수점을 가장 왼쪽으로 이동시켜 0.1101로 만들고, 소수점을 어떻게 옮기면 원래 수인 1.101로 이동시킬 수 있는지 고민해본다. 오른쪽으로 +1 옮기면 되므로 3bit 초과 표기법에 따라 101₍₂₎을 지수 부분에 넣는다. 부호 비트는 양수이므로 0을 넣는다. 최종적으로 부동소수점 표기법을 사용해 완성한 값은 01011101₍₂₎이다.
다음으로 00111100₍₂₎와 01000110₍₂₎의 경우를 생각해보자. 부동소수점으로 해석하면 전자의 지수부분은 011₍₂₎, 유효숫자는 1100₍₂₎, 후자는 100₍₂₎, 0110₍₂₎이다. 둘다 0 + .011 즉, 3/8의 값을 가리킨다. 하지만 유효숫자의 가장 첫번째 값이 1로 시작하는 전자의 경우를 정규형(normalized form)이라고 하고 동일한 값에 대해 여러 가지 표현이 생길 가능성을 피할 수 있다.
절단 오차(Truncation Errors)
무한소수와 같은 숫자의 경우 아무리 많은 자리수를 사용하더라도 정확히 표현될 수 없다. 따라서 식을 어느 정도 자른 근사값을 사용하게 되는데 이때 오차가 발생한다.
1byte 부동소수점 체계에서 2 + 5/8을 저장하려고 할 때, 2진법 표현을 먼저 구하면 10.101₍₂₎이 된다. 이제 지수 부분을 구하기 위해 위의 수를 전부 유효숫자 필드로 넘기게 되면 문제가 발생한다. 유효숫자 필드는 4자리에 불과한데 들어가야할 수는 .10101로 5자리다. 이렇게 되면 어쩔 수 없이 가장 마지막 수를 잃어버리게 되고 이대로 나머지 과정을 지속하면 01101010₍₂₎이 되고 이는 2 + 1/2이다. 이렇게 부동소수점 체계에서는 저장한 값이 원래 값과 달라지는 경우가 생기는데 이를 절단 오차(Truncation Errors)라고 한다.
오늘날의 대부분의 컴퓨터는 위의 예시처럼 부동소수점 체계로 값을 저장할 때 8bit가 아니라 최소 32bit를 사용해 지수 필드와 유효숫자 필드를 늘려서 사용한다. 하지만 아무리 더 길게 늘려도 정밀도가 충분하지 않은 경우가 있다.
절단 오차의 또 다른 원인으로는 1/3, 1/17과 같은 무한소수 문제가 있다. 10진법의 경우에도 이러한 무한소수 문제가 존재하는데 2진법에는 10진법보다 더 많은 무한소수가 존재한다. 대표적으로 2진법에서 0.1도 무한소수다.

각설하고 부동소수점 표기법으로 표현된 숫자를 더할 때, 더하는 순서가 중요하다. 그렇다고 이러한 절단 오차가 발생하지 않는다는 보장은 없지만 최대한 작은 값들부터 더해서 큰 값에 더해질 때 절단되지 않을 정도의 값이 되기를 바라야 한다. 대부분의 경우 32bit체제 머신 이상의 정밀도를 요하는 작업이 없을 수 있지만 그래도 이러한 부분을 유념하고 있어야 한다.
'프로그래밍 > Computer Science' 카테고리의 다른 글
| [Overview] 02. Data Manipulation - (1) Computer Architecture and Machine Language (0) | 2023.07.17 |
|---|---|
| [Overview] 01. Data Storage - (4) Data Compression (0) | 2023.07.14 |
| [Overview] 01. Data Storage - (2) Main Memory (0) | 2023.07.11 |
| [Overview] 01. Data Storage - (1) Bit 그리고 Bit의 저장 (0) | 2023.07.09 |
| [알고리즘] 02. 에라토스테네스의 체 (4) | 2023.05.19 |
